Deep learning その 2: Parameter Optimization

机器学习的一般框架是：建立模型，确定目标（损失）函数，使用最优化算法进行参数求解。

那么，神经网络当然也遵循这个基本的流程。

不同模型的损失函数评判标准不一。

例如感知机、SVM的损失函数仅由误分类点决定，即正确分类的点对参数更新没有帮助。

而Logistics回归的极大似然损失、神经网络常用的交叉熵损失则是概率模型，即使正确分类，若预测概率值与目标不相等，损失函数值仍不为零。

那么对于神经网络，初始化网络权重，根据具体的损失函数得到当前的loss后，要如何把loss最小化，即要如何进行网络中全部参数的求解呢？

答案是基于梯度的迭代方法，每一层网络参数的梯度都可以通过BP算法计算得到，那么有了梯度方向，就可以使用经典的SGD进行参数的迭代更新。

1 梯度计算

BP算法（Error Backpropagation），我的理解就是链式法则，不过因为前层网络的梯度对后层网络存在依赖关系，所以从后往前计算，避免重复计算。

假设输入为2维特征，回归问题的损失函数为MSE损失，对下面的神经网络简单推导如下。

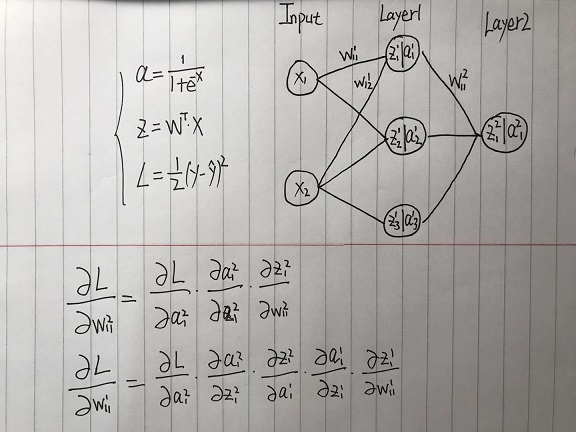
那么因为BP中的求导是基于链式法则，当网络层数过深时，为小数的梯度值不断累乘，会造成梯度弥散。

针对梯度弥散，解决方案有以下两个：ReLU、BN。

ReLU

S型函数如Sigmoid、Tanh函数在输入过小或过大时，梯度值变得非常小，那么将其替换为ReLU族函数则不存在这个问题，虽然新的问题是ReLU易坏死。

BN

也可以从scale的角度入手，将输入值拉伸到合适的范围，避免出现过大或过小值。

2 参数を更新

2.1 SGD

神经网络普遍采用SGD，即随机梯度下降（Stochastic Gradient Descent），作为最优化方法。

SGD是GD的变体，关于梯度下降法GD，我在这篇文章里有介绍。$\rightarrow$ Logistic Regression

GD是沿着整个训练集的梯度方向下降，而SGD则是随机挑选小批量数据进行梯度下降。

那么SGD这样改进的优点在哪里呢？

速度快
引入随机性，一定程度上可以避免局部最小值

在算法实现上，有别于原始SGD，主流框架都是通过epoch来实现这种随机性。即设定一个小批量数据的数目batch_size，依次去遍历训练集，经过数次迭代后将训练集全部遍历一遍就是一个epoch。

2.2 SGD with Momentum

SGD-M的下降方向不再仅由此时的梯度决定，而是由历史梯度 $g_{t-1}$ 和此时梯度 $g_t$ 构成的动量 $m_t$ 共同决定。

简单讲历史梯度就是一个惯性，而当前梯度负责对这个惯性做微调。

定义：待优化参数 $\theta$，目标函数 $f(\theta)$，学习率 $\alpha$，动量衰减系数 $\beta_1$。

超参数 $\beta_1$ 一般取值0.9

那么更新策略如下，在每次迭代 $t$：

计算当前梯度：$g_t=\nabla f(\theta_t)$
计算当前动量（下降方向）：$m_t=\beta_1\cdot m_{t-1}+(1-\beta_1)\cdot g_t$
更新参数：$\theta_{t+1}=\theta_t-\alpha \cdot m_t$

2.3 AdaGrad

Ada是Adaptive的缩写，AdaGrad对SGD的改进在学习率上。

AdaGrad引入了二阶动量以自适应不同参数的学习率，所谓二阶动量就是该参数所有历史梯度值的平方和$V_t=\sum_{i=1}^t g_i^2$，学习率反比于此二阶动量。其作用是在参数空间中越平缓的倾斜方向，使用越大的学习率。（Deep Learning Book 原文：Greater progress in the more gently sloped directions of parameter space.）

Q：为什么要在平缓的倾斜方向上使用大学习率？

A：我的理解是加入此二阶动量后，对那些历史梯度较大的参数，降低其学习率以防止震荡；而历史梯度较小的参数即 gently sloped directions，仍可以使用大学习率进行更新。

（无论优化的结果是好是坏，随着历史梯度的积累到一定程度，对应参数的更新都是趋于停滞的。简单讲就是配额制，步长配额用完的参数就停止更新。）

定义：待优化参数$\theta$，目标函数$f(\theta)$，学习率$\alpha$。

未引入额外超参数。

那么更新策略如下，在每次迭代$t$：

计算当前梯度：$g_t=\nabla f(\theta_t)$
计算当前二阶动量：$V_t=\sum_{i=1}^t g_i^2$
更新参数：$\theta_{t+1}=\theta_t-\cfrac{\alpha}{\sqrt V_t} \cdot g_t$

2.4 AdaDelta

与AdaGrad一样使用二阶动量来自适应不同参数的学习率，不同的地方在于AdaDelta改进了二阶动量的计算方式。加入了二阶动量衰减系数 $\beta_2$ ，避免了AdaGrad在初始梯度太大时造成之后学习率一直过低的情况。

二阶动量计算方式： $V_t=\beta_2*V_{t-1}+(1-\beta_2)g_t^2$

定义：待优化参数 $\theta$，目标函数 $f(\theta)$，学习率 $\alpha$，二阶动量衰减系数 $\beta_2$。

超参数 $\beta_2$ 一般取值0.9

那么更新策略如下，在每次迭代$t$：

计算当前梯度：$g_t=\nabla f(\theta_t)$
计算当前二阶动量：$V_t=\beta_2*V_{t-1}+(1-\beta_2)g_t^2$
更新参数：$\theta_{t+1}=\theta_t-\cfrac{\alpha}{\sqrt V_t} \cdot g_t$

2.5 Adam

同时引入一阶动量和二阶动量，并且针对其初始值为零的情况，进行了数值矫正。

定义：待优化参数 $\theta$，目标函数 $f(\theta)$，学习率 $\alpha$，一阶动量衰减系数 $\beta_1$，二阶动量衰减系数 $\beta_2$。

超参数 $(\beta_1, \beta_2)$ 一般取值(0.9, 0.999)

那么更新策略如下，在每次迭代$t$：

计算当前梯度：$g_t=\nabla f(\theta_t)$
计算当前一阶、二阶动量：$m_t=\beta_1\cdot m_{t-1}+(1-\beta_1)\cdot g_t$，$V_t=\beta_2*V_{t-1}+(1-\beta_2)g_t^2$
计算一阶、二阶动量矫正值：$\hat{m_t}=\cfrac{m_t}{1-\beta_1^t}$，$\hat{V_t}=\cfrac{V_t}{1-\beta_2^t}$
更新参数：$\theta_{t+1}=\theta_t-\cfrac{\alpha}{\sqrt {\hat V_t}} \cdot \hat{m_t}$

3 权重衰减

权重衰减（weight decay）是优化器中的可选项，其等价于在损失函数中加入$L_2$范数作为正则项。关于正则项，我在这篇文章里有介绍。$\rightarrow$ Generalization in Machine Learning

为什么优化器中的权重衰减等价于$L_2$范数正则项？

首先$L_2$范数的公式为$\lVert x\rVert_2=\sqrt{\sum_i x_i^2}$。

假设原始损失函数为 $f(\theta)$，那么加入$L_2$正则项（为方便计算对$L_2$范数做了一些变形）后损失函数为$g(\theta)=f(\theta)+\cfrac{\lambda}{2\alpha}\lVert\theta\rVert_2^2$。

相应在SGD优化过程中，迭代公式变为：

\[\begin{align} \theta_{t+1} &= \theta_t-\alpha \cdot \nabla g(\theta_t)\\ &= \theta_t-\alpha\cdot(\nabla f(\theta_t)+\frac{\lambda}{\alpha}\theta_t)\\ &= \theta_t-\alpha\cdot\nabla f(\theta_t)-\lambda\theta_t \end{align}\tag{あ}\]

可以看出，加入 $L_2$ 正则项后，迭代公式的变化是多了一项 $-\lambda\theta_t$，因此将其称为权重衰减，超参数$\lambda$即是权重衰减系数。