Generalization in Machine Learning
机器学习中的泛化能力，指模型对未知数据（测试集）的拟合能力。
从统计学习的角度出发，具体的学习策略有两种方案：经验风险最小（ERM）和结构风险最小（SRM）。
- 经验风险最小 Empirical Risk Minimization， 仅考虑模型在已知数据（训练集）上的表现，经验风险最小的模型就是最优的模型。在数据量足够大的，ERM能够保证有很好的学习效果；但是当数据量不足时，ERM学习出来的模型往往会出现过拟合的现象，即仅在训练集上表现好，而在测试集上表现差。
- 结构风险最小 Structural Risk Minimization，是为了防止过拟合而提出的策略，在ERM的基础上加入正则项（惩罚项）对模型的复杂度进行约束，以提升模型的泛化能力。
以下图的二分类问题为例，以ERM的标准，倾向于绿色曲线；而以SRM的标准，黑色曲线则是最优选择。
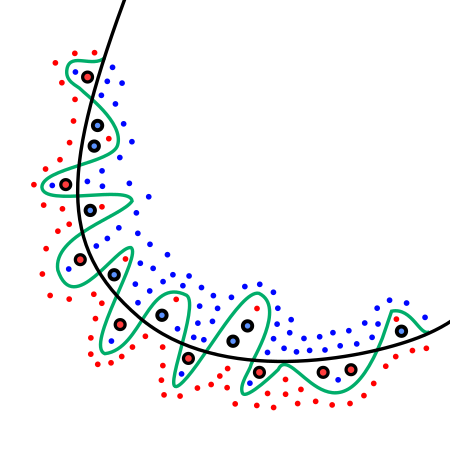
以下我将简单介绍在机器学习的不同阶段，评估/提升模型泛化能力的方法。
1 模型训练
模型训练阶段，从SRM的角度考虑，需要对模型加一个正则项。正则项的选取，常用的有L1、L2范数。
L1范数，也称为曼哈顿范数，为参数向量元素绝对值之和。以L1范数作为正则项，目的是使模型稀疏化，防止模型参数过多。例如 lasso regression 就是在线性回归的基础上加L1范数作为正则项。
\[\lVert x \rVert_1 = \sum_i \vert x_i \rvert \tag{1}\]L2范数，也称为欧几里得范数，为参数向量元素绝对值平方和再开方。以L2范数作为正则项，防止参数过拟合到某个特征上。例如 ridge regression 就是在线性回归的基础上加L2范数作为正则项。
\[\lVert x \rVert_2 =\sqrt{ \sum_i x_i^2}\tag{2}\]2 模型选择
模型选择考虑的是不同的模型之间的优劣。
从ERM的角度考虑，拟合数据最好的模型，即似然函数值$\hat L$最大的模型是最好的。那么从SRM的角度考虑，是寻求一个模型复杂度与拟合数据之间的最佳平衡。以SRM策略为目标的评分准则，常用的有AIC、BIC评分。
Akaike Information Criterion 由
日本人赤池（ Akaike）于1974年提出，$k$是模型参数的个数，$\hat L$是似然函数值，AIC评分越小模型越好。
Bayesian Information Criterion 由Schwarz 于1978年提出，$k$是模型参数的个数，$n$是样本数量，$\hat L$是似然函数值，BIC评分越小模型越好。对比AIC，BIC的改进是考虑了样本数量$n$，大数据量时，惩罚项更大。
\[{\rm BIC}=k\ln(n)-2\ln(\hat L)\tag{4}\]3 Bagging
Bagging是集成学习（ensemble learning）策略的一种。
集成学习的思想是利用多个弱分类器组合一个强分类器，主要有bagging和boosting两种策略。Boosting的目标是提升分类器拟合能力，而bagging则是为了提升分类器的泛化能力。
Bagging策略的做法是对样本均匀随机重采样，对每一份重采样得到的子样本训练一个模型，利用得到的N个模型进行最终的结果预测。
Reference
[1] 李航 (2012) 统计学习方法. 清华大学出版社, 北京.