Logistic Regression

Updated in March 06, 2019

逻辑回归（LR）是机器学习中的经典分类方法。

简单理解就是在线性回归+sigmoid激活函数，从而把分类问题转变为回归问题。

1 Logistic 回归模型

首先介绍Logistic 函数，由比利时人 Pierre Verhulst 于1845年研究模仿人口增长的曲线时发现并命名。其数学形式如下：

\[y=\frac{L}{1+e^{-k(x-x_0)}}\]

机器学习中常用的激活函数 sigmoid 函数（Sigmoid 意为S型），一般特指 logistic 函数的简化形式。其数学形式及函数曲线如下，值域为 $(0, 1)$。

\[y=\frac{1}{1+e^{-x}}\tag{1}\]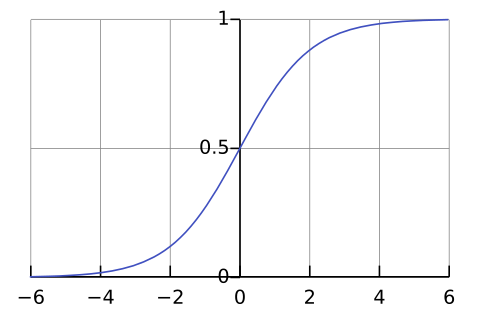

进入正题，Logistic 回归模型的数学形式如下：

\[p(y=1|x,\theta)=\frac{1}{1+e^{-\theta^Tx}}\tag{2}\]

Logistic 回归的输出是一个概率值，根据此概率值与阈值 $μ$ 的大小进行分类，$μ$ 一般取值0.5。

若 $p(y=1|x,\theta)>μ$，则 $y^*=1$。函数具有对称性质，$p(y=0|x,\theta)=1-p(y=1|x,\theta)$。

因为线性回归残差服从高斯分布，所以可以使用最小二乘法进行参数求解；而 Logistic 回归的因变量、残差均为二项分布，不满足正态性，所以使用MLE为目标函数来进行参数$\theta$的求解。

2 最大似然估计（MLE）

最大似然估计Maximum Likelihood Estimation，是一个用来估计概率模型参数的方法，由英国人 Ronald Fisher 于上世纪20年代推广。MLE的两个条件是已知数据和概率分布假设（似然函数），其思想是求得这个分布具有什么样的参数值才能使我们观测到这组数据的可能性最大。

假设有一组独立同分布(i.i.d.)的随机变量 $X={x_1,x_2,\cdots,x_n}$，给定一个概率分布 $D$，假设其概率密度函数为 $f$，那么通过参数为 $\theta$ 的模型 $f$ 产生上面这组样本的概率为:

\[f(x_1,x_2,\cdots,x_n|\theta)=\prod_{i=1}^n f(x_i|\theta)\]

MLE寻找使得这组样本出现的概率最大的参数 $\theta$。也就是根据样本估计参数$\theta$，定义似然函数为：

\[L(\theta|x_1,x_2,\cdots,x_n)=f(x_1,x_2,\cdots,x_n|\theta)=\prod_{i=1}^n f(x_i|\theta)\]

取对数后，对数似然函数如下：

\[l(\theta)=\sum_{i=1}^n \ln f(x_i|\theta)\tag{3}\]

最大似然估计即最大化对数似然函数 $l(\theta)$，$\theta^*=\mathop{\arg \max}_\theta l(\theta)$。

3 损失函数

那么具体到 Logistic 回归，样本标签 $y_i$ 取值为0或1，预测概率值为 $h_{\theta}(x)=\cfrac{1}{1+e^{-\theta^Tx}}$。

则似然函数为如下形式：

\[L(\theta|x_1,x_2,\cdots,x_n)=\prod_{i=1}^n h(x_i)^{y_i}(1-h(x_i))^{1-y_i}\]

取对数后，对数似然函数为：

\[l(\theta)= \sum_{i=1}^n [y_i\ln h(x_i)+(1-y_i)\ln (1-h(x_i))]\tag{4}\]

在不引入正则项的情况下，Logistic 回归的目标函数是最小化负的平均对数似然函数，如下：

\[J(\theta)=-\frac{1}{n}l(\theta)\]

由于多元变量很难求得解析解 $\theta^=\mathop{\arg \min}_\theta J(\theta)$，一般使用梯度下降法逼近 $\theta^$ 的最优值。

4 梯度下降法

梯度下降法 Gradient Descent 是最优化算法的一种，据说由法国人 Augustin Cauchy 于1847年提出。从函数当前点对应梯度的反方向按一定的步长$\alpha$进行迭代搜索，寻找函数$J(\theta)$的一个局部极小值点。若目标函数为凸函数，则得到的一定是全局最小值点。

GD 算法如下：

1）随机指定初始值 $\theta^k$，$k=0$

2) 以全部数据为样本计算当前点 $\theta^k$ 的梯度，即对每个 $\theta_i$ 求偏导

\[g^k_i=\frac{\partial J(\theta)}{\partial\theta_i}\tag{5}\]

3) 更新$\theta$值，迭代公式如下

\[\theta^{k+1}_i=\theta^k_i-\alpha g^k_i\tag{6}\]

4) 若函数 $J(\theta)$ 未收敛到极小值点，则令 $k=k+1$，重复步骤2、3；若已收敛，则停止迭代。

5 调包淆

from sklearn import linear_model, datasets
from sklearn.model_selection import train_test_split

def LR_demo():
    # load datasets
    iris = datasets.load_iris()
	X = iris.data[:, :2]  # use the first two features
	Y = iris.target
    X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=0)
    
    # fit model
	lr_model = linear_model.LogisticRegression(C=1e3)
	lr_model.fit(X_train, Y_train)
    
    # predict
	acc = lr_model.score(X_train,Y_train)
	prepro = lr_model.predict_proba(X_train)
    print acc, prepro