Image Interpolation

0 为什么需要插值（Interpolation）？

一个简单的例子，若将一张图像绕原点旋转30度，旋转后的图像上点 $(1,1)$ 对应的原图像点 $(x,y)$ 是哪一个呢？

原坐标点 $(x,y)$ 可以通过计算出仿射变换矩阵后，解线性方程组求得。

\[\begin{bmatrix} 0.866 & 0.5 & 0\\ -0.5 & 0.866 & 0 \end{bmatrix}\cdot \begin{bmatrix} x\\y\\1 \end{bmatrix}= \begin{bmatrix} 1\\1 \end{bmatrix}\]

最终求得点 $x=0.366, y=1.366$ 。

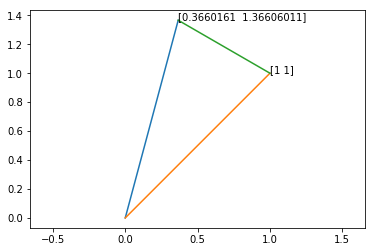
然而图像坐标是离散的，点 $(0.366,1.366)$ 在原图像上并不存在，新坐标点 $(1,1)$ 也就无法找到在原图像上对应的坐标点。

在对图像进行缩放（resize）、旋转（rotation）等操作时常常出现这种情况。

此时需要根据其周围的点对未知点进行像素插值，常见的插值方法有以下几种。

1 传统插值方法

void resize(InputArray src, OutputArray dst, Size dsize, double fx=0, double fy=0, int interpolation=INTER_LINEAR)

OpenCV中提供了五种插值（interpolation）方法。

INTER_NEAREST - 最近邻插值
INTER_LINEAR - 双线性插值（缺省值）
INTER_CUBIC - 双立方插值
INTER_AREA - 区域插值
INTER_LANCZOS4 - a Lanczos interpolation over 8x8 pixel neighborhood

其中最常用的插值算法是最近邻、双线性、双立方三种，其原理如下图所示。

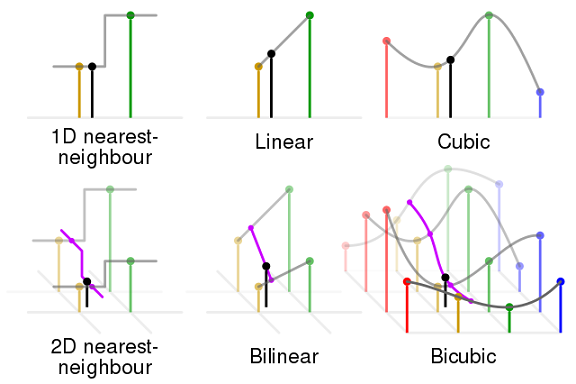
1.1 最近邻插值

以待插值点 $(x,y)$ 周围 $2\times2$ 区域内的4个点为依据进行插值。

最近邻插值不产生新的像素值，而是将与其欧式距离最近的点的像素直接赋值给点 $(x,y)$。

1.2 双线性插值

以待插值点 $(x,y)$ 周围 $2\times2$ 区域内的4个点为依据进行插值。

双线性插值是一种基于相对距离的加权平均。

假设待插值点 $(x,y)$ 周围4个点像素值分别为 $f(x_0,y_0),f(x_0,y_1),f(x_1,y_0),f(x_1,y_1)$，则先进行 $x$ 方向上插值，再进行 $y$ 方向插值，最终映射关系如下：

\[f(x,y_0) = \cfrac{x_1-x}{x_1-x_0}f(x_0,y_0)+\cfrac{x-x_0}{x_1-x_0}f(x_1,y_0)\\ f(x,y_1) = \cfrac{x_1-x}{x_1-x_0}f(x_0,y_1)+\cfrac{x-x_0}{x_1-x_0}f(x_1,y_1)\\ f(x,y) = \cfrac{y_1-y}{y_1-y_0}f(x,y_0)+\cfrac{y-y_0}{y_1-y_0}f(x,y_1)\]

双线性插值与最近邻插值相比虽然计算量有所增加但插值效果更加平滑，因而是OpenCV中的默认插值方法。

1.3 双立方插值

以待插值点 $(x,y)$ 周围 $4\times4$ 区域内的16个点为依据进行插值。

利用了更多的像素点并采用更复杂的插值函数，所以效果会比双线性插值更平滑，计算代价也更大。

2 转置卷积

以上传统插值算法所使用的都是人工定义好的映射关系。

当然我们也能以机器学习的方式从数据中学习得到自适应的映射关系。

处理图像语义分割任务的 FCN 模型便使用了转置卷积（transposed conv）, 也有人称之为 deconv，来对图像进行上采样（upsampling），即图像放大。

在介绍转置卷积原理之前，我们首先以矩阵乘法的形式再来认识一下卷积（convolution）。

定义卷积核尺寸 kernel_size=2，步长 stride=1，padding=0，对尺寸为 $3\times3$ 的图像 $X$ 进行卷积可以得到尺寸为 $2\times2$ 的图像 $Y$。将二维图像展开到一维，则卷积可以用矩阵乘法表示如下，矩阵 $W$ 即代表上述卷积操作：

\[W \cdot X = \begin{bmatrix} w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0 & 0\\ 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0\\ 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0\\ 0 & 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 \end{bmatrix}\cdot \begin{bmatrix} x_1\\x_2\\x_3\\ x_4\\x_5\\x_6\\ x_7\\x_8\\x_9 \end{bmatrix}= \begin{bmatrix} y_1\\y_2\\ y_3\\y_4 \end{bmatrix} = Y\tag{1}\]

定义卷积核尺寸 kernel_size=2，步长 stride=1，padding=2，对图像 $Y$ 进行卷积操作可以得到与原图像 $X$ 尺寸相同的图像 $X’$。同样将二维图像展开到一维，则矩阵 $W’$ 代表上述卷积操作：

\[W' \cdot Y = \begin{bmatrix} w'_4 & 0 & 0 & 0\\ w'_3 & w'_4 & 0 & 0\\ 0 & w'_3 & 0 & 0\\ w'_2 & 0 & w'_4 & 0\\ w'_1 & w'_2 & w'_3 & w'_4\\ 0 & w'_1 & 0 & w'_3\\ 0 & 0 & w'_2 & 0\\ 0 & 0 & w'_1 & w'_2\\ 0 & 0 & 0 & w'_1\\ \end{bmatrix}\cdot \begin{bmatrix} y_1\\y_2\\ y_3\\y_4 \end{bmatrix}= \begin{bmatrix} x'_1\\x'_2\\x'_3\\ x'_4\\x'_5\\x'_6\\ x'_7\\x'_8\\x'_9 \end{bmatrix} = X'\tag{2}\]

可以观察到，矩阵 $W$ 和矩阵 $W’$ 在形状上互为转置矩阵。

转置卷积，即指对原图像进行卷积得到的小尺寸的 feature map 再卷积上采样到原图像尺寸。

注意，矩阵 $W$ 和矩阵 $W’$ 参数并无对应关系。