Softmax loss から、ArcFace まで
1 背景
人脸识别,作为图像识别的一个子领域,本质上还是一个多分类任务。
神经网络中处理多分类任务($n$类)的模式是固定的:
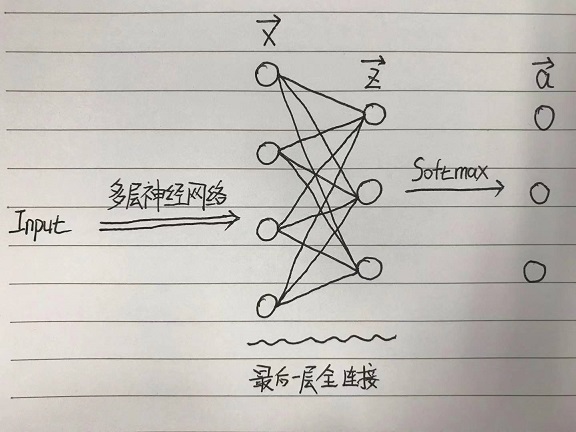
- 使用多层神经网络对输入进行特征提取,最终得到一个 $n$ 维向量 $\vec{z}$ ;
- 使用Softmax函数对 $n$ 维向量进行归一化 $\vec{z} \rightarrow \vec{a}$ ,将 $\vec{a}$ 与对应的label求得交叉熵损失;
- 将交叉熵损失BP回去更新网络参数、优化所提取到的分类特征。
在这个固定模式下,可以在三个方向上进行优化:数据、网络结构、损失函数。
本篇涉及到的所有文章都是对softmax损失函数的改进。
1.1 Softmax+交叉熵损失
对 $n$ 维向量进行归一化 $\vec{z} \rightarrow \vec{a}$ ,Softmax函数形式如下:
\[a_i(\vec{z})=\cfrac{e^{z_i}}{\sum_{j=1}^n e^{z_j}},{\rm for}\quad i=1,\dots,n\]而交叉熵损失(CrossEntropyLoss)定义如下:
\[L=-\sum_i^n y_ilna_i\]$\vec{y}$ 向量为输入样本对应label的one-hot编码,所以 $\vec{y}$ 只有一个维度的值为1,其他维度的值皆为0。
那么假设 $y_i=1$,将Softmax函数带入后的交叉熵损失形式如下:
\[\begin{aligned} L_s &= -lna_i \\ &=-ln\cfrac{e^{z_i}}{\sum^n_{j=1} e^{z_j}} \end{aligned}\]我们的目标是 $L_s=0$,即让 $a_i=1$,那么最终的优化目标则是让 $z_i$ 取值尽可能的大。
1.2 类内距离损失
这个方向上的开坑之作,Center loss (ECCV2016),首先对基于Softmax损失函数得到的特征进行了可视化。
这里可视化的特征是倒数第二层神经元,即最后一层全连接的输入 $\vec{x}$ 。
将最后一层全连接用线性变换表示,$z_i=W^T_i \cdot x$,那么Softmax损失函数可以改写成如下形式:
\[L_S=-ln\cfrac{e^{W^T_ix}}{\sum^n_{j=1} e^{W^T_jx}}\]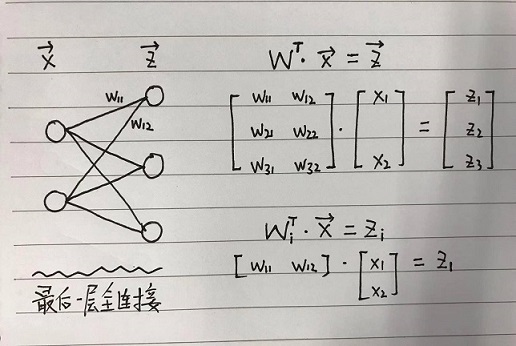
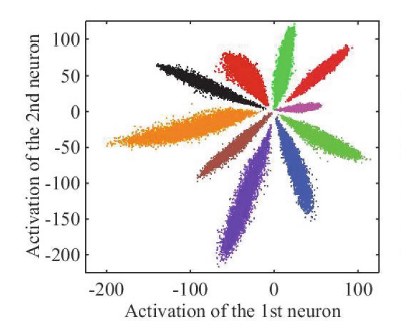
下图是论文中给出的可视化结果,将倒数第二层神经元个数置为2,得到可视化的二维特征。
我的复现结果也与之类似。
观察Softmax损失函数得到的特征,每一类的类内距离明显是可以减小的。
所以作者在Softmax损失函数的基础上,增加了一个惩罚项 $L’$ 来减小特征间的类内距离。因此,此方法仅适用于每一类有多个样本的数据集。
\[L = L_S + \lambda L'\tag{1}\]Center loss基于欧式距离所定义的类内距离损失 $L’$ 如下:
\[L_C = \cfrac{1}{2}\sum^m_{i=1}\Vert x_i-c_{y_i}\Vert^2_2\]Softmax损失函数加入Center loss约束后,学习到的特征可视化如下:
总结一下,Center loss这篇文章的核心贡献有两个:
1、发现了可以对类内距离损失 $L’$ 进行约束;
2、并提出了一个基于欧式距离的类内距离损失。
下面介绍的三篇文章,都是在Center loss思路的基础上,基于余弦距离或角度距离来重新定义类内距离损失 $L’$ 。
- L-Softmax loss, ICML2016
- A-Softmax loss, CVPR2017
- ArcFace, arXiv2018
2 L-Softmax loss
使用欧式距离对类内距离损失进行约束是合适的吗?
L-Softmax loss (ICML2016),提出用余弦距离代替欧式距离,然后增大学习的难度。
对于二分类,Softmax的决策边界是 $W^T_1x>W^T_2x$,而向量点积可以用几何定义来表示:$\vec{a} \cdot \vec{b}=\Vert a\Vert \Vert b\Vert \cos\theta$。因此,Softmax的决策边界可以转化为如下形式:
\[\Vert W_1\Vert \Vert x\Vert \cos\theta_1>\Vert W_2\Vert \Vert x\Vert \cos\theta_2\]然后引入一个参数 $m$ 来增大学习的难度,因为cos函数在 $[0, \pi]$ 范围内单调递减,所以 $m$ 取值范围为正整数。相应的决策边界为:
\[\Vert W_1\Vert \Vert x\Vert \cos m\theta_1>\Vert W_2\Vert \Vert x\Vert \cos\theta_2\]最终,L-Softmax loss的定义如下:
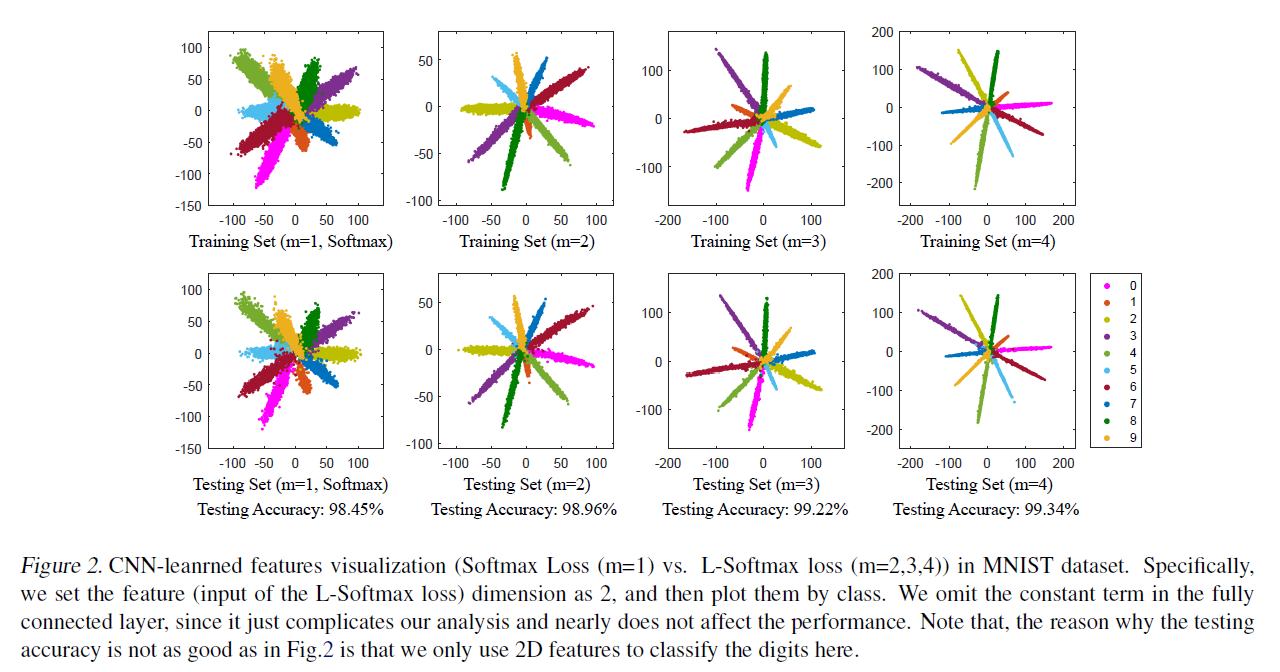
\[L=-ln\cfrac{e^{\Vert W_i\Vert \Vert x\Vert \cos m\theta_i}}{e^{\Vert W_i\Vert \Vert x\Vert \cos m\theta_i} + \sum^n_{j=1,j\neq i} e^{\Vert W_j\Vert \Vert x\Vert \cos \theta_j}}\tag{2}\]基于 L-Softmax loss 学习到的特征可视化如下:
3 A-Softmax loss
A-Softmax loss 是 SphereFace (CVPR2017) 提出的一个方法。
因为余弦距离衡量的是空间中两个向量的夹角,与向量长度无关。
所以在 L-Softmax loss 的基础上,A-Softmax loss 索性对参数向量 $\Vert W_i\Vert$ 进行了L2归一化。
其决策边界为如下形式:
\[\Vert x\Vert(\cos m\theta_1-\cos\theta_2)=0\]相应的,L-Softmax loss 定义如下:
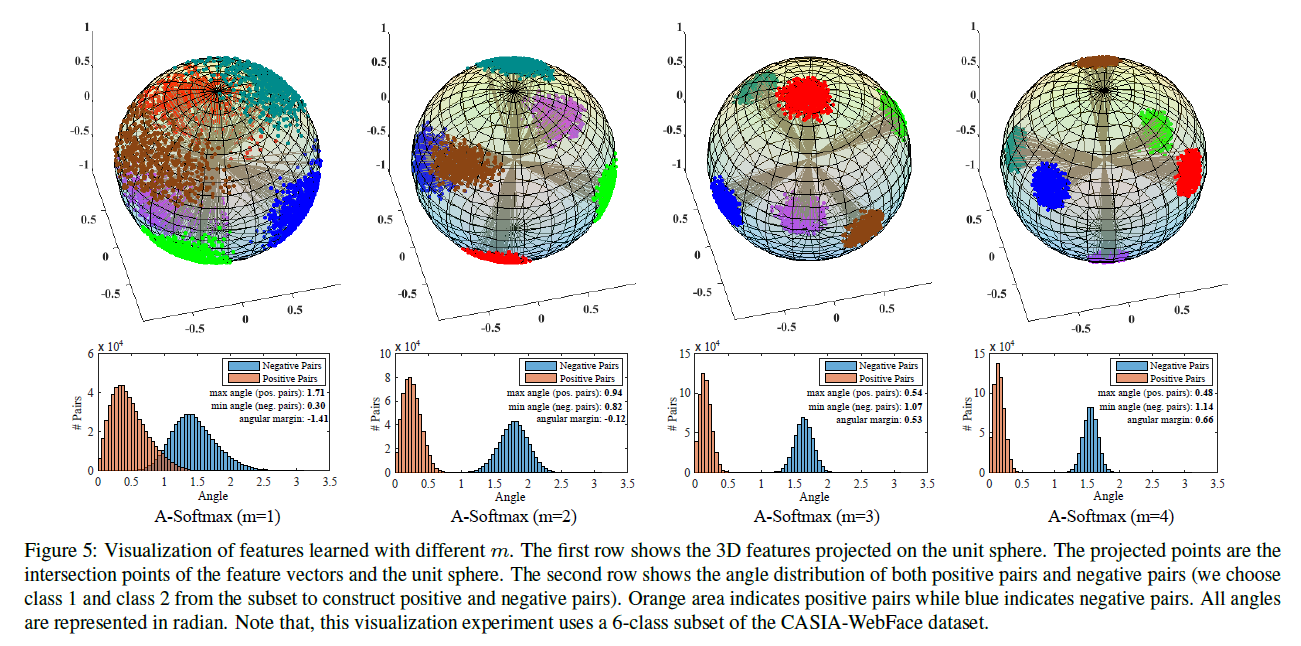
\[L=-ln\cfrac{e^{\Vert x\Vert \cos m\theta_i}}{e^{\Vert x\Vert \cos m\theta_i} + \sum^n_{j=1,j\neq i} e^{\Vert x\Vert \cos \theta_j}}\tag{3}\]基于 A-Softmax loss 学习到的三维特征可视化如下:
4 ArcFace
终于到 ArcFace 了。
ArcFace 的改进是,在 SphereFace 对参数向量 $\Vert W_i\Vert$ 进行归一化的基础上,对特征 $\vec{x}$ 也做了L2归一化。
因此,决策边界变成了如下形式:
\[s(\cos(\theta_1+m)-\cos \theta_2)=0\]相应的,L-Softmax loss 定义如下:
\[L=-ln\cfrac{e^{s(\cos (\theta_i+m))}}{e^{s(\cos (\theta_i+m))} + \sum^n_{j=1,j\neq i} e^{s(\cos \theta_j)}}\tag{4}\]关于超参数
关于超参数 $m$ 的取值,作者基于实验给出的建议是 0.2~0.5(弧度值),取值大于0.5时会过拟合。
关于数据集
| Dataset | identities # | images # |
|---|---|---|
| VGG2 | 9,131 | 3.31M |
| MS-Celeb-1M | 100k | 10M |
| LFW | 5,749 | 13.23k |
| CFP | 500 | 7k |
| AgeDB | 440 | 12.24k |
| MegaFace | 690k | 1M |
训练集:VGG2, MS-Celeb-1M;验证集:LFW, CFP, AgeDB;测试集:MegaFace。
(验证集的作用是选择超参数。)
Reference
[2] A Discriminative Feature Learning Approach for Deep Face Recognition, ECCV2016
[3] Large-Margin Softmax Loss for Convolutional Neural Networks, ICML2016
[4] SphereFace: Deep Hypersphere Embedding for Face Recognition, CVPR2017
[5] ArcFace: Additive Angular Margin Loss for Deep Face Recognition, arXiv2018