Affine, Perspective Transformation

1 仿射变换

仿射变换是在二维空间上对图像进行平移、缩放、旋转、shear 和镜像5个操作的组合。

仿射变换后，相交线之间的角度可能发生变化（shear），但平行线之间的关系保持不变。

因为仿射变换是在二维空间中进行的，所以至少需要3个点才能构造一个 $2\times3$ 的仿射变换矩阵。

仿射变换矩阵中各个元素的作用见下图：

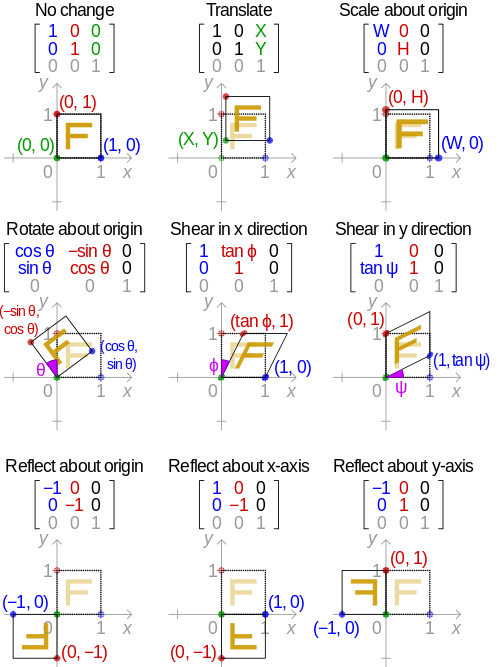
求出仿射变换矩阵 $M$ 后，与点 $P(x, y)$ 进行矩阵乘法，就得到仿射变换后的点 $P’(x’,y’)$。

\[M \cdot \begin{bmatrix} x\\y\\1 \end{bmatrix}= \begin{bmatrix} x'\\y' \end{bmatrix}\] \[\begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 2 \end{bmatrix}\cdot \begin{bmatrix} 0\\0\\1 \end{bmatrix}= \begin{bmatrix} 1\\2 \end{bmatrix}\] \[\begin{bmatrix} 0 & 1 & 0\\ -1 & 0 & 0 \end{bmatrix}\cdot \begin{bmatrix} 0\\1\\1 \end{bmatrix}= \begin{bmatrix} 1\\0 \end{bmatrix}\]

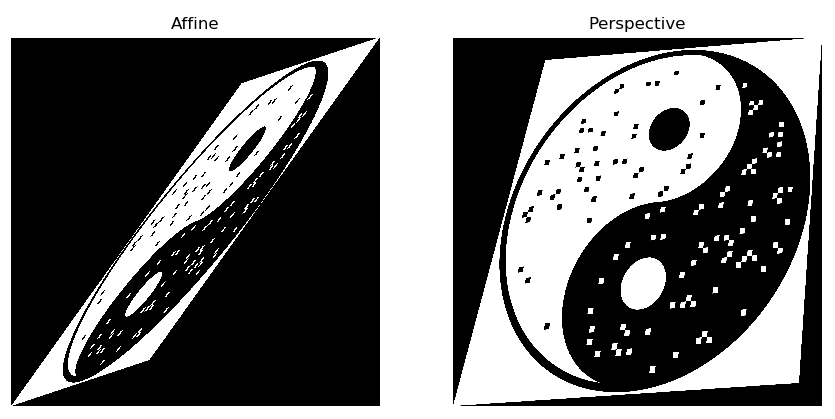
2 透视变换

“一个简单的例子，你用手电筒往墙上打光。

如果手电筒和墙面垂直，打出来的光是圆，有倾斜角度就是椭圆。离墙面近光环就小点，离得远光环就大点。

但手电筒本身是固定不变的，只是不同的透视变换有不同的结果。”

透视变换就是通过投影的方式，把当前平面上的图像映射到另外一个平面。

因为透视变换是在三维空间中进行的，所以至少需要4个点才能构造一个一个 $3\times3$ 的透视变换矩阵。

透视变换矩阵没有直观的理解，就不做解释辽。

3 OpenCV中调用

import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt

img = cv.imread('circle.jpg')
# affine
pts1 = np.float32([[0,0], [3200,0], [0,3200]])
pts2 = np.float32([[2400,200], [3200,0], [0,3200]])
M = cv.getAffineTransform(pts1,pts2)
dst = cv.warpAffine(img,M,(3200,3200))
plt.imshow(dst, cmap=plt.cm.gray)
plt.show()

# perspective
pts1 = np.float32([[0,0], [3200,0], [0,3200], [3200, 3200]])
pts2 = np.float32([[800,200], [3200,0], [0,3200], [3000, 3000]])
M = cv.getPerspectiveTransform(pts1,pts2)
dst = cv.warpPerspective(img,M,(3200,3200))
plt.imshow(dst, cmap=plt.cm.gray)
plt.show()

Reference

[1] Wikipedia Affine transformation

[2] OpenCV Geometric Transformations of Images

[2] 仿射变换与投影变换 - houkai