1 GAN是什么?
Generative adversarial nets,生成对抗式网络,Ian Goodfellow 2014年提出的模型。
简单来讲就是定义两个神经网络模型,一个是验钞机、一个假币生成机,以对抗博弈的方式来彼此学习进步,最终达到生命的大和谐(误)。
基础架构
$r$:真实数据;
$z$:随机噪声,服从分布$p_z(z)$;
$G(z)$:生成器,用神经网络去生成仿造数据;
$D(x)$:判别器,判定$x$来自真实数据的概率。
最终目标
$G(z)$ 学到的分布和真实数据分布相同,$p_g=p_r$,让 $D(x)$ 无法区分 $G(z)$ 与真实数据,即 $D(x)=\frac{1}{2}$。
2 如何优化?
2.1 GAN的优化目标
\[\min_G \max_DV(D,G)=E_{x\sim p_r}[\log D(x)]+E_{x\sim p_g}[\log(1-D(x)]\tag{1}\]2.2 minimax算法
问题背景是零和博弈。
假设有A,B两个玩家,双方利益之和为零或一个常数,那么任一方的获利必然意味着对方的损失。
令A玩家得分为$V$,那么A玩家目标是最大化$V$。对于博弈问题,在A玩家做出最优解的同时,也要假设对手是有智商的,所以B玩家目标是最小化$V$。
\[\min_B \max_A V\]Minimax算法就是在A的回合最大化$V$,在B的回合最小化$V$,以一定深度交替计算求出最优解。
所以GAN的优化目标,式$(1)$,也是分解为两个部分来进行。
2.3 两个子优化目标
1 判别器:最大化$D(x)$的正确分类率
\[\max_D V(D,G)=E_{x\sim p_r}[\log D(x)]+E_{x\sim p_g}[\log(1-D(x)]\tag{2}\]2 生成器:最小化$D(x)$的正确分类率
\[\begin{aligned} \min_G V(D,G)&= E_{x\sim p_g}[\log(1-D(x)]\\ &= E_{z\sim p_z(z)}[\log(1-D(G(z))] \end{aligned}\tag{3}\]3 PyTorch实现
实现代码基于莫烦的 GAN 教程,有改动。
$r$:以介于一定范围的二次函数作为真实数据。$y=ax^2+a-1, a\sim U[1,3]$,并从 $[-2,2]$ 均匀取 DATA_COMPONENTS 个点,作为一个函数的抽样;
$z$:$z\sim N[0,1]$,因为直接使用 torch.randn() 生成随机数,而这个函数使用标准正态分布(见文档);
$G(z)$:两层神经网络;
$D(x)$:两层神经网络。
完整代码如下:
# -*- coding: utf-8 -*-
"""
Created on Tue Oct 30 20:00:14 2018
@author: Yonji
"""
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
BATCH_SIZE = 64
LR_G, LR_D = 0.0001, 0.0001 # learning rate for G, D
NOISE_COMPONENTS = 5 # G的输入维度、即噪声维度
DATA_COMPONENTS = 15 # G的输出维度、同时也是D的输入维度、即真实数据维度
# x轴坐标点、[-1, 1]之间等分、再复制batch_size个
PAINT_POINTS = np.array(
[np.linspace(-2, 2, DATA_COMPONENTS) for _ in range(BATCH_SIZE)])
# real data
def artist_works():
# lower & upper bound
a = np.random.uniform(1, 3, size=BATCH_SIZE)[:, np.newaxis]
paintings = a * np.power(PAINT_POINTS, 2) + a - 1
paintings = torch.from_numpy(paintings).float()
return paintings
class GNet(nn.Module):
def __init__(self):
super(GNet, self).__init__()
self.fc1 = nn.Linear(NOISE_COMPONENTS, 128)
self.fc2 = nn.Linear(128, DATA_COMPONENTS)
def forward(self, x):
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
class DNet(nn.Module):
def __init__(self):
super(DNet, self).__init__()
self.fc1 = nn.Linear(DATA_COMPONENTS, 128)
self.fc2 = nn.Linear(128, 1)
def forward(self, x):
x = F.relu(self.fc1(x))
x = torch.sigmoid(self.fc2(x))
return x
if __name__ == "__main__":
D, G = DNet(), GNet()
opt_D = torch.optim.Adam(D.parameters(), lr=LR_D)
opt_G = torch.optim.Adam(G.parameters(), lr=LR_G)
plt.ion()
for epoch in range(401):
artist_paintings = artist_works() # real data
G_ideas = torch.randn(BATCH_SIZE, NOISE_COMPONENTS) # z
G_paintings = G(G_ideas) # G(z)
# 论文公式、MLE loss
prob_real = D(artist_paintings)
prob_fake = D(G_paintings)
D_loss = - torch.mean(torch.log(prob_real) + torch.log(1. - prob_fake))
G_loss = torch.mean(torch.log(1. - prob_fake))
# Loss BP、更新参数
opt_D.zero_grad()
D_loss.backward(retain_graph=True) # reusing computational graph
opt_D.step()
opt_G.zero_grad()
G_loss.backward()
opt_G.step()
# plotting
if epoch % 100 == 0:
plt.cla()
plt.plot(PAINT_POINTS[0], 3 * np.power(PAINT_POINTS[0], 2) + 2,
"--", c='#000066', lw=2, label='upper bound of data')
plt.plot(PAINT_POINTS[0], 1 * np.power(PAINT_POINTS[0], 2) + 0,
"--", c='#4AD631', lw=2, label='lower bound of data')
plt.plot(PAINT_POINTS[0], artist_paintings.data.numpy()[0],
c='#0066ff', lw=3, label='a real data')
plt.plot(PAINT_POINTS[0], G_paintings.data.numpy()[0],
c='red', lw=3, label='G(z)')
plt.text(-1.2, 10, 'epoch = %d' % epoch, fontdict={'size': 14})
plt.text(-1.2, 9, 'D_accuracy = %.2f' %
prob_real.data.numpy().mean(), fontdict={'size': 14})
plt.text(-1.2, 8, 'D_loss = %.2f' %
D_loss.data.numpy(), fontdict={'size': 14})
plt.ylim((0, 14))
plt.legend(loc='upper right', fontsize=10)
plt.draw();plt.pause(0.02)
plt.ioff()
plt.show()
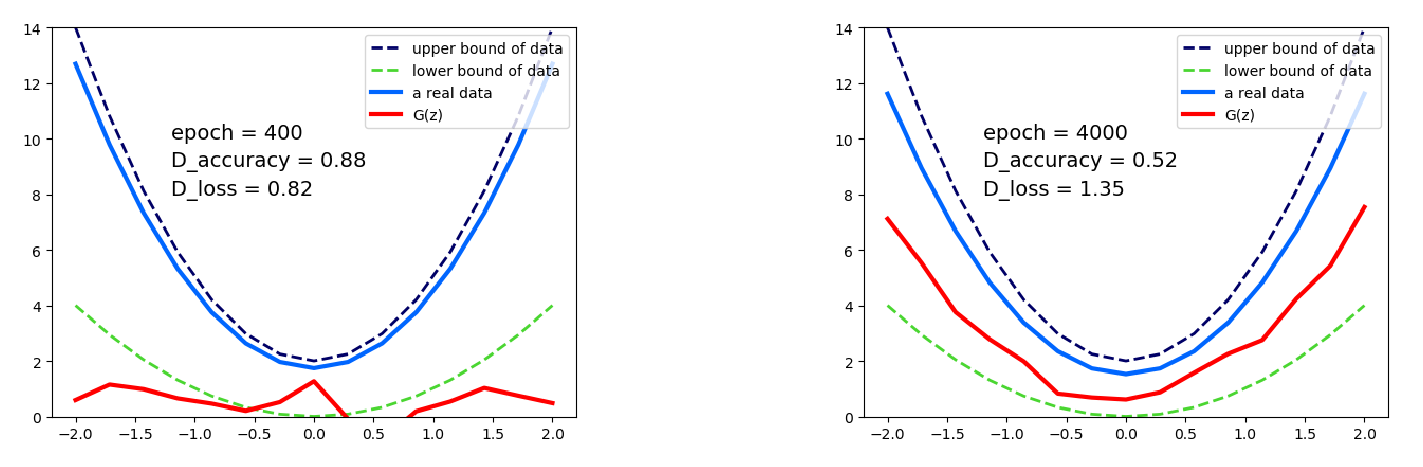
结果如下图:
4 このディオだ!
WRYYYYYYYYYY!