PCA

主成分分析（Principal Component Analysis）是机器学习里一个基础的降维方法，由英国人Karl Pearson于1901年提出。其实现原理是通过正交化线性变换，将数据从原来的坐标系转换到新的坐标系，我自己的理解PCA本质是坐标系旋转。

新坐标系由数据分布所决定。第一个新坐标轴是原始数据中方差最大的方向；第二个新坐标轴选择与第一个坐标轴正交且方差最大的方向；重复此过程直至新坐标与原坐标维度（特征）数目相同。新坐标轴的重要程度依次递减，因此能够将降维的信息损失最小化。

1 PCA算法

以上是PCA的直观理解，具体到算法实现，如下4个步骤：

输入：数据矩阵$A$，矩阵形状$M\times N$，代表$M$个样本、$N$个维度。

计算转置矩阵$A^T$的协方差矩阵$\sum$（因为目标是特征而非样本，所以这里是矩阵$A$的转置）；
对协方差矩阵进行特征分解，$\sum=Q\Lambda Q^{-1}$；
将$\Lambda$中的特征值降序排序，再将$Q$中每列对应的特征向量重新排列后得到矩阵$P$；
将数据转换到新的坐标系，$A’=AP$。

输出：新数据矩阵$A’$，矩阵形状$M\times N$，$N$个维度的主成分依次递减。

$\clubsuit$ 在NumPy中，如何计算协方差矩阵、进行方阵的特征值分解，参见我这篇笔记。$\rightarrow$ NumPy Notes

以上就是PCA算法的计算过程，非常简单。

从直观理解到算法实现之间的公式推导，待补充。

2 Python实现

2.1 调包淆

以iris数据集为例，使用sklearn中的PCA函数对比变换前后的数据维度。

# -*- coding: utf-8 -*-
"""
Created on Sun Aug 19 11:13:34 2018
@author: Yonji
"""
from sklearn import datasets
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
# data
iris = datasets.load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names

# model
pca = PCA()
X_r = pca.fit(X).transform(X)

# show result
print('explained variance ratio (all 4 components): %s'
      % str(pca.explained_variance_ratio_))

plt.subplot(121)
colors = ['navy', 'turquoise', 'darkorange']
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X_r[y == i, 0], X_r[y == i, 1], color=color, label=target_name)
plt.title('PCA axis 0 and 1')
plt.legend()

plt.subplot(122)
colors = ['navy', 'turquoise', 'darkorange']
for color, i, target_name in zip(colors, [0, 1, 2], target_names):
    plt.scatter(X[y == i, 0], X[y == i, 1], color=color, label=target_name)
plt.title('Original axis 0 and 1')
plt.legend()

plt.show()

结果如下图，左图是PCA的前两个主成分，右图是原始数据的前两个维度。

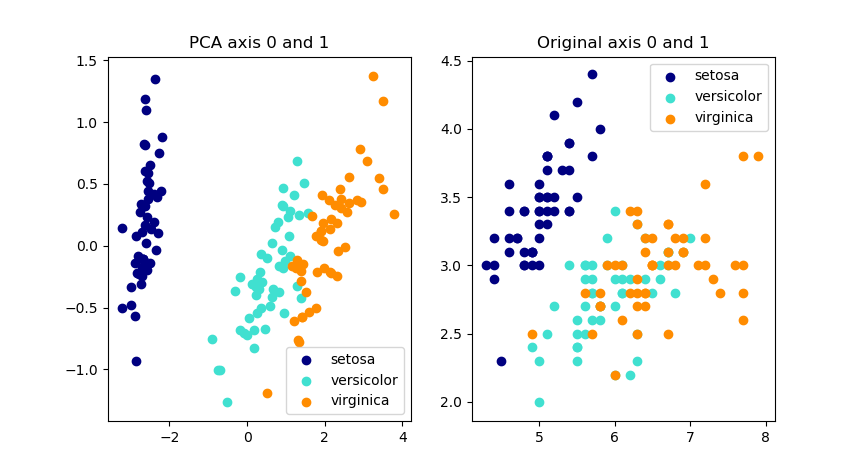
2.2 NumPy手动实现

以下是我自己写的PCA实现

import numpy as np
def PCA_Yonji(X):
    # 1
    cov = np.cov(X.T)
    # 2
    va, ve = np.linalg.eig(cov)
    # 3
    order = np.argsort(-va)
    P = ve[:,order]
    # 4
    X_s = np.dot(X, P)
    # zero-center data
    m = np.mean(X_s, axis=0)
    X_s -= m
    return X_s

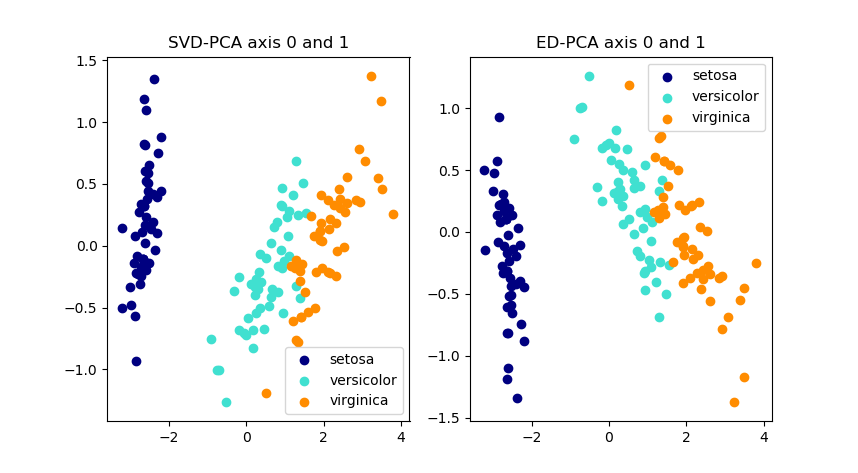
同样使用上面的iris数据集，验证的结果如下图。

对比sklearn中的PCA函数，我们自己写的这个版本，某些维度发生了符号反转，这是因为sklearn所使用的是奇异值分解（SVD），而非特征值分解（ED）。

3.1 LDA

线性判别分析（Linear Discriminant Analysis），英国人Ronald Fisher于1936年提出的一个经典分类方法。

LDA和PCA的相同点在于，算法本质都是线性降维。不同的是PCA是为了降维而降维，而LDA的目标是分类。经过线性变换后，让数据在低维空间上的类内方差最小、类间方差最大。

3.2 AE

自动编码器（AutoEncoder），利用神经网络来进行非线性降维。设定隐层神经元少于输入维度，再将输入作为隐层神经元输出的拟合目标。それでは、编码过程は$Input \rightarrow HiddenLayer$です；解码过程は$HiddenLayer \rightarrow Output$です。