CNN Notes
Updated in Mar 01, 2019.
卷积神经网络(Convolutional Neural Networks),深度学习三巨头之一 法国人 Yann LeCun 的杰作,在图像识别领域具有统治级的优秀表现。
法国人 Yann LeCun 的杰作,在图像识别领域具有统治级的优秀表现。
卷积神经网络不断推陈出新,从 AlexNet (2012)、VGGNet (2014)、InceptionV2 (2015)、ResNet(2015),现在已经趋于稳定。
这篇笔记简单介绍一下这些网络结构的两个共同基础,卷积层和池化层。
1 卷积层(Convolution Layer)
$\star$ 使用多层神经网络的优势是可以提取输入数据(例如图像)的高维特征。
在介绍卷积层之前,我们首先来看使用普通的全连接层会怎样呢,对一张 $224\times224$ 的单通道灰度图像,一个神经元需要学习的参数量(省略偏置项)为 50176。
而对于卷积层,一个神经元的参数量仅为一个卷积核的大小,通常为 $3\times3,5\times5, 7\times7$,那么参数量就下降了三个数量级。
那么卷积核是什么呢?
卷积核本质是一个线性滤波(filter),例如均值滤波、高斯滤波等,使用卷积核以一定的步长在整个图像上滑动,就得到了图像的一个feature。因为是以同一个卷积核对整个图像的不同部分进行扫描,所以对于整个图像来说不同部分之间是权值共享的。
那么使用多个卷积核就能得到多个feature,再使用ReLU等非线性激活函数来达到提取图像各种高维特征的目的。
以下是 Stanford CS231n所给出的卷积层计算过程的例子:
输入为 $5\times5\times3$ 的RBG三通道图像矩阵 $x$。
卷积层有两个神经元,其卷积核分别为 $w_0$ 和 $w_1$,每个卷积核都是一个 $3\times3\times3$ 的滤波矩阵。(卷积核最后一个维度值和输入图片通道数相等,相当于每个通道上 $5\times5$ 的图片都有一个 $3\times3$ 的滤波。)
当然一般不同通道间是使用相同的卷积核,但无论不同通道间是否共享卷积核,一个神经元对应位置的输出值都是此卷积核在所有输入信道上的卷积值之和。
除了卷积核的尺寸外,对图像进行扫描还需要额外定义的两个参数:
- stride,卷积核在原始图像上扫描时的步长。
- padding,边缘填充,在原始图像边缘填充的个数。
PyTorch中的卷积层
class torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1, bias=True)
以上是PyTorch中一个2D的卷积层定义,必须指定的参数有三个:in_channels, out_channels, kernel_size。
- in_channels,输入信道,上一层神经元的个数。若为第一层,则对于RGB三通道图像数据,这个值为3。
- out_channels,输出信道,此卷积层神经元的个数,即卷积核的数目。
- kernel_size,卷积核尺寸。
假设输入图像为 $C_{in}\times W_1\times H_1$;
定义卷积层神经元个数为 $C_{out}$,每个神经元卷积核尺寸为$F\times F$,填充位数padding为$P$,步长stride为$S$;
则此卷积层的输出维度为$W_2\times H_2\times K$,其中$W_2=\cfrac{W_1-F+2P}{S}+1, H_2=\cfrac{H_1-F+2P}{S}+1$。
那么如果想让卷积后的图片尺寸保持不变,一般设$S=1,P=\cfrac{F-1}{2}$。
2 池化层(Pooling Layer)
池化层的作用是降维,池化层并没有需要学习的参数,因此一般讲并不计算在网络层数中。
降维对于神经网络这样参数量较大的模型优点有两个:一是使优化更容易,二是提升模型的泛化能力。
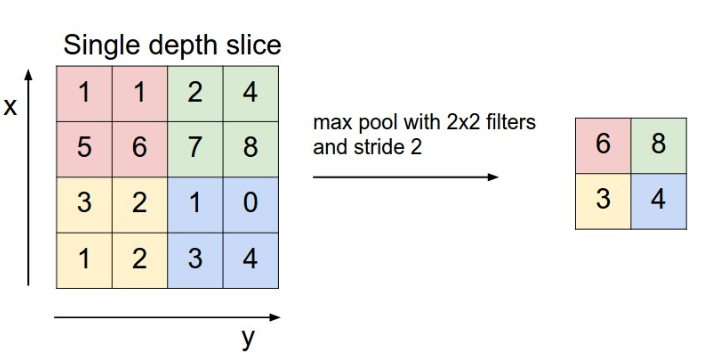
池化的方式有很多,常用的是 max pooling,即选择区域内最大的元素值作为对应位置的输出。
PyTorch中的池化层
class torch.nn.MaxPool2d(kernel_size, stride=None, padding=0, dilation=1, return_indices=False, ceil_mode=False)
以上是PyTorch中一个2D的最大值池化层定义,必须指定的参数有两个: kernel_size, stride。
- kernel_size,卷积核尺寸。
- kernel_size,步长。
$\star$ 注意,如果池化后的维度数不是整数,会向下取整。
例如 nn.MaxPool2d(2, 2),尺寸 $7\times7$ 的图像池化后变为 $3\times3$ 。
3 PyTorch demo
下段代码定义了一个拥有3个卷积层、3个全连接层,总深度为6的神经网络。
目的是展示一下,如果不使用padding的话,计算feature map的size是一件多么让人捉急的事。
输入数据为$32\times32$的三通道图像,即输入维度$3\times32\times32$;多分类标签有10个,即输出维度为10。
我们需要计算最后一层卷积层的输出维度$C\times H\times W$,来给全连接层的输入维度赋值,以下为此维度的计算过程。
- Step1,第1层卷积神经元个数为6,卷积核为$3\times3$,则此层输出维度为$6\times30\times30$;
- Step2,第2层卷积神经元个数为12,卷积核为$3\times3$,则此层输出维度为$12\times28\times28$;
- Step3,池化层池化核为$2\times2$,步长为2,则此层输出维度为$12\times14\times14$;
- Step4,第3层卷积神经元个数为24,卷积核为$3\times3$,则此层输出维度为$24\times12\times12$;
- Step5,池化层池化核为$2\times2$,步长为2,则此层输出维度为$24\times6\times6$。
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.pool = nn.MaxPool2d(2, 2)
self.conv1 = nn.Conv2d(3, 6, 3)
self.conv2 = nn.Conv2d(6, 12, 3)
self.conv3 = nn.Conv2d(12, 24, 3)
# C*H*W
self.fc1 = nn.Linear(24 * 6 * 6, 120)
self.fc2 = nn.Linear(120, 84)
self.fc3 = nn.Linear(84, 10)
def forward(self, x):
# 1-2
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = self.pool(x)
# 3
x = F.relu(self.conv3(x))
x = self.pool(x)
# reshape
x = x.view(-1, 24 * 6 * 6)
# fully connected
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
Reference
[1] 李航 (2012) 统计学习方法. 清华大学出版社, 北京.