Deep learning その 1: Activation Function

神经网络中，一个节点的激活函数定义了此节点输入与输出之间的映射关系。

0 Perception

神经网络（Neural Networks）与感知机（Perceptron）很大的区别，或者说改进就在于激活函数的不同。

简单介绍一下，感知机模型由美国心理学家Frank Rosenblatt 于1958年提出，是一个处理二分类问题的线性模型，同时也是SVM、Logistics回归和神经网络的基础。模型如下：

对于线性不可分的数据，感知机模型无法收敛。Sign函数，也称单位跃迁函数，常用形式如下：

\[f(x)={\rm sign}(x)=\begin{cases}+1,x>0\\-1,x\leq0\end{cases}\tag{1}\]

而神经网络常使用如 Sigmoid、Tanh、ReLU 等可导的非线性函数作为神经元的激活函数。

为什么要使用非线性的激活函数，因为若激活函数为线性，则无论神经网络有多少层，输出都是输入的线性组合，多层没有任何意义。因此引入非线性的激活函数，神经网络才有理论上拟合任意函数的能力。

1 Sigmoid函数

Sigmoid函数，也称S型函数，数学表达式如下：

\[f(x)=\frac{1}{1+e^{-x}}\tag{2}\]

Sigmoid函数将任意范围内的输入映射在 [0, 1] 区间内。优点是求导简单，$f’(x)=f(x)(1-f(x))$。

但缺点是因为S型函数的关系，在输入值较大或较小时梯度值过小。

import math
def sigmoid(x):
    return 1.0 / (1 + math.exp(-x))
def sg(x):
    f = sigmoid(x)
    g = f * (1 - f)
    print('x={:2d}, g={:.4f}'.format(x, g))
for i in range(0, 11, 2):
    sg(i)
'''
x= 0, g=0.2500
x= 2, g=0.1050
x= 4, g=0.0177
x= 6, g=0.0025
x= 8, g=0.0003
x=10, g=0.0000
'''

2 Tanh函数

Tanh函数，即双曲正切函数，数学表达式如下：

\[f(x)=\tanh(x)=\frac{\sinh(x)}{\cosh(x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}\tag{3}\]

Tanh 函数与 Sigmoid 函数同为S型函数，区别是其将输出映射在 [-1, 1] 区间内。

3 ReLU函数

线性整流单元（Rectified Linear Unit）,也称斜坡函数，数学表达式如下：

\[f(x)=\max(0,x)\tag{4}\]

ReLU 函数提出以后基本取代了 Sigmoid 函数的地位，其优点是节省计算量（在激活区间内梯度值为1），在保留激活函数非线性能力的同时避免了梯度消失；缺点是在非激活区间梯度值为0，权重将不再更新，造成『死节点』出现。

4 GELU函数

高斯误差线性单元（Gaussian Error Linear Unit），是16年提出的一个对ReLU的改进，因在 GPT、BERT 中的应用而被NLP领域广泛采用，数学表达式如下：

\[f(x)=x\cdot\Phi(x)\tag{5}\]

$\Phi(x)$ 为正态分布的累积分布函数，数学表达式为 $\Phi(x)=\cfrac{1}{2}[1+{\rm erf}(x/\sqrt2)]$，其中 ${\rm erf}$ 为误差函数。

GELU函数可以近似如下：$f(x)\approx x*\sigma(1.702x)$，$\sigma(x)$ 为sigmoid函数。

5 Swish函数

Swish 是 Google 17年的一个工作，通过强化学习进行激活函数的搜索，因在 EfficientNet 中的应用而被CV领域广泛采用，数学表达式如下：

\[f(x)=x\cdot\sigma(x)\tag{6}\]

$\sigma(x)$ 为sigmoid函数，可以看到 Swish 就是去掉系数 1.702 的GELU近似。。。

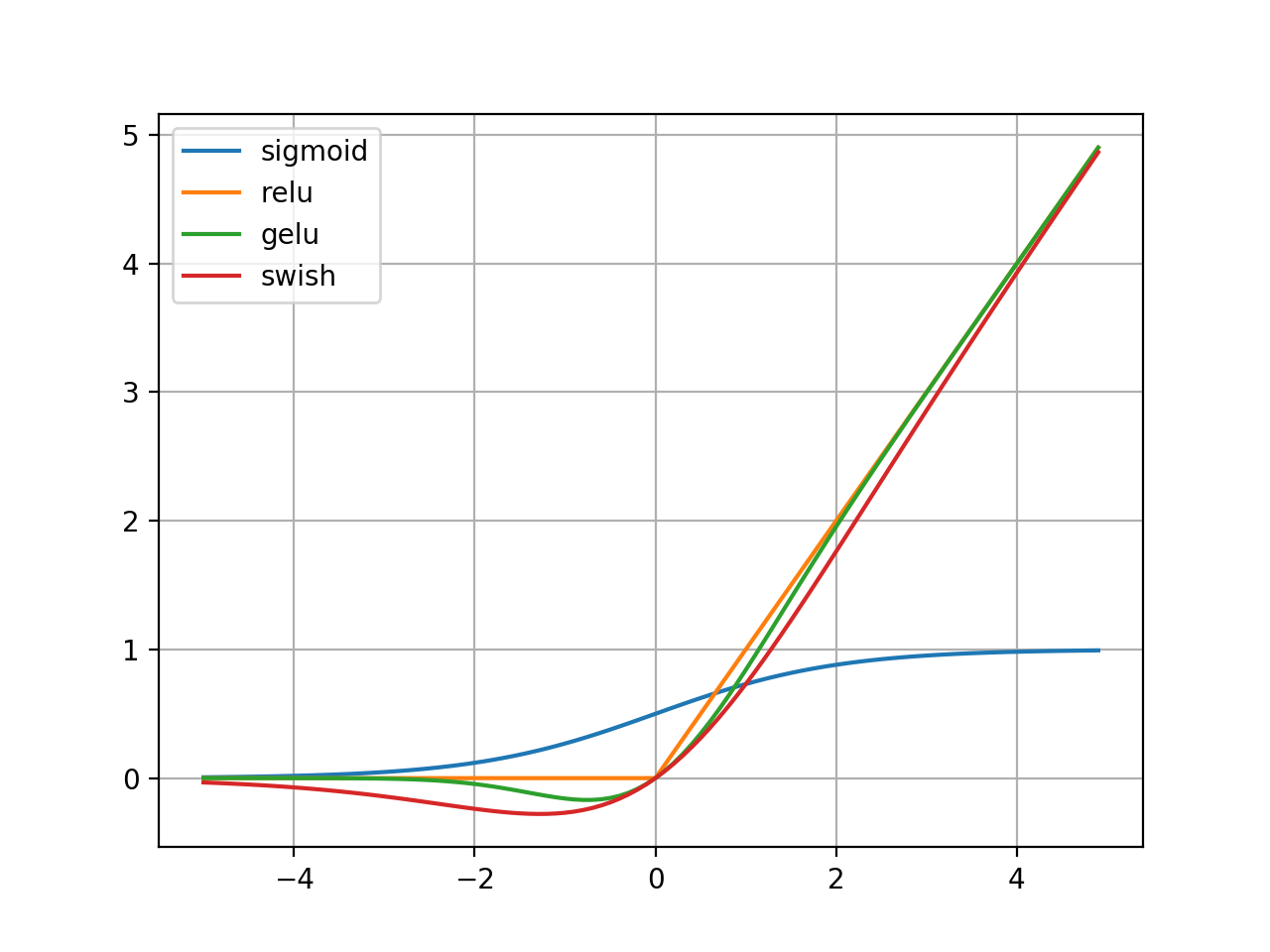
画了个图，可以直观对比一下常用的激活函数。

import math
from scipy.special import erf
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1.0 / (1 + math.exp(-x))
def relu(x):
    return max(0, x)
def gelu(x):
    return x * 0.5 * (1 + erf(x / math.sqrt(2))) 
def swish(x):
    return x * sigmoid(x)

def compare():
    x = np.arange(-5, 5, 0.1)
    y_sigmoid = [sigmoid(e) for e in x]
    y_relu = [relu(e) for e in x]
    y_gelu = [gelu(e) for e in x]
    y_swish = [swish(e) for e in x]
    plt.plot(x, y_sigmoid, label='sigmoid')
    plt.plot(x, y_relu, label='relu')
    plt.plot(x, y_gelu, label='gelu')
    plt.plot(x, y_swish, label='swish')
    plt.legend()
    plt.grid()
    plt.show()
compare()

activation_compare

6 Softmax函数

Softmax函数常用于多分类神经网络的最后一层，对输出向量进行归一化。

将一个元素为任意实数的 $n$ 维向量 $\vec{z}$ 压缩为一个同为 $n$ 维的向量 $\vec{a}$，向量$\vec{a}$中原始值域范围为[0, 1]，且元素和为1。Softmax归一化会放大原始输入值之间的差异。

数学形式如下：

\[a_i(\vec{z})=\cfrac{e^{z_i}}{\sum_{j=1}^n e^{z_j}}，{\rm for}\quad i=1,\dots,n\tag{7}\]

import math
def softmax(z):
    z = [math.exp(e) for e in z]
    the_sum = sum(z)
    return [(e / the_sum) for e in z]

print(softmax([1, 2]))
# 0.2689414213699951, 0.7310585786300049]

Reference

[1] Wikipedia Activation Function

[2] 从感知机到深度神经网络-机器之心

[3] 深度学习-从线性到非线性-徐阿衡

[4] GELU https://arxiv.org/abs/1606.08415

[5] Swish https://arxiv.org/abs/1710.05941

Yonji's Blog| Home