超越机器学习：因果推断与do-算子介绍

本文翻译自剑桥大学博士Ferenc Huszár的博文，原文标题为：ML beyond Curve Fitting: An Intro to Causal Inference and do-Calculus，原文链接。

你或许偶然看到了Judea Pearl的新书（The Book of Why，2018年5月出版），并且与之相关的采访在社交网站上被点赞之交们广泛分享。Pearl在采访里把我们在机器学习上的大多数工作贬为仅仅在做曲线拟合。虽然我相信这是夸大其词的说法，但大多数有意义的辩论常常是由富有争议性或者自大的言论引起的。最近一个很好的例子就是将机器学习比作炼金术。在读过文章后，我决定再次研究一下Pearl著名的“do-算子”和因果推断。

之所以说再一次，是因为我之前已经接触过很多次了。第一次学到“do-算子”是在本科时期一次贝叶斯网络的课上，这门课不怎么受欢迎但是很高级就行了。自此，我每隔2到3年都要在不同的领域接触到“do-算子”，但我从来没有真正对此感兴趣过。我的想法仅仅是“这玩意太难了吧，也许还没什么卵用”，最终都是与之擦身而过。直到现在，我才意识到这个东西是有多么的基础。

p3：我信了，我入教。

p4：不但入教，我还要传教。

1 基础知识

首先，causal calculus 差别对待两种看似一样的条件分布。太长不看版：机器学习中，我们通常只关注其中一个，但一些应用场景下我们实际上应该试着去估计另一个，或者说我们必须这么做。

假设我们有从$p(x,y,z,\dots)$得到的独立同分布的数据抽样，我们有大量的数据和最好的工具（深度学习）来充分估计它们的联合分布或者是条件分布、边缘分布这样的属性，简单讲就是$p$已知且易处理。我们感兴趣的是在给定$x$的条件下，变量$y$的表现。高级一点的说法，你可以以两种方式问这个问题：$p(y|x)$，$p(y|do(x))$。 观察型 $p(y|x)$：观察到变量$X$取值为$x$时$Y$的概率分布。对于有监督机器学习，我们通常是这么做的。这是一个基于$p(x,y,z,\dots)$可以被计算的条件分布，即两个边缘分布的比值，$p(y|x)=\cfrac{p(x,y)}{p(x)}$。我们对这个分布和计算方法非常熟悉。 干预型 $p(y|do(x))$：将变量$X$强行设置为$x$时$Y$的概率分布。这个描述的是如果我强行干预$X$的取值为$x$，模拟其他变量按照原始机制产生相应数据时$Y$的分布。（注意这里的数据生成部分和$p(x,y,z,\dots)$是不同的，这一点非常重要）。

2 这两个有什么不一样？

不，很不一样。你可以通过做几组实验来验证这一点。假设$Y$是我咖啡机水壶内的压力，取值范围为0到1.1，取决于运行时间。$X$是咖啡机内置气压计的显示值。在随机时间同时观察$X$，$Y$。合适的气压计函数$p(y|x)$应当是一个均值为$x$的单峰（unimodal）分布，随机性由测量误差体现。然而，$p(y|do(x))$实际上并不依赖于$x$的取值，其大体上等于水壶压力的边缘分布$p(y)$。因为我们人工设置了气压计的显示值（比如将指针固定），这并不会改变水壶内真实的压力值。

总结一下，$y$和$x$是相关的或者说统计上是有依赖关系的，因此可以由观察到的$x$去预测$y$。但$y$的值并不是由$x$决定的，所以设定$x$的值并不会对$y$的分布造成影响。这个例子只是冰山一角，在多个变量存在复杂交互影响时，观察型条件性和干预型条件性的差别可以是更加细微和难以描述的。

3 我想要哪一个？

取决于你想要解决的问题，你应该设法去估计其中的一个。如果你的终极目标是诊断或者预测（即以观察到的自然产生的$x$来推测$y$的值），那么你需要的就是$p(y|x)$。这就是我们在有监督学习中所做的事，也就是 Juda Pearl 所说的曲线拟合。这适用于一系列重要应用：分类、图像分割、高分辨率成像、语音识别和机器翻译等等。 如果你的终极目标是基于预计的条件分布来控制或者选择$x$的值，那么你应该使用$p(y|do(x))$。例如，如果$x$是药物治疗，$y$是治疗结果，那么你并不仅满足于观察自然产生的治疗$x$和结果预测。我们想要的是在$x$会影响$y$的假设下，来主动选择$x$。相似的应用场景有系统识别、控制和在线推荐系统。

4 $p(y|do(x))$到底是什么？

这或许是我以前没有理解的主要概念。$p(y|do(x))$实际上是一个香草（vanilla）条件分布，但并不基于$p(x,y,z,\dots)$计算，相反是一个不同的分布$p_{do(X=x)}(x,y,z,\dots)$。$p_{do(X=x)}$就是假如我们采取干预后得到的数据分布。$p(y|do(x))$就是我们在随机控制实验中控制变量$x$后得到的条件分布。需要注意的是真的去采取干预或者随机实验或许是不可能的，或者说至少在实践层面或者伦理层面是是不可能的。即使你不能在随机实验上直接估计$p(y|do(x))$，但这个问题依然存在。因果推断和“do-算子”的重心就是：如果我不能通过随机控制实验测量$p(y|do(x))$，那么我可以从无干预的观察数据上去估计它吗？

5 所有这些是怎么联系到一起的？

让我们从这副图开始，如果我们只关心$p(y|x)$，即下面这个简单的有监督学习例子：

假设我们观察到3个变量$x,y,z$，观察数据是联合分布的独立同分布抽样。我们的关注点是以$x$预测$y$，$z$变量同样可以测量但不进行操作（考虑到完整性）。观察到的条件概率$p(y|x)$可以从联合分布计算得到。具体可以使用深度学习来最小化交叉熵或者其他方法，从训练数据构建一个模型$p(y|x,\theta)$来近似这个条件概率。 如果我们关心的是$p(y|do(x))$，如下图

我们仍有观察到的联合分布（蓝色所示），数据同样是此联合分布的抽样。然而我们希望估计的是右下角的干预概率$p(y|do(x))$。这取决于上方的因子图（红色所示）。这是一个源自$p(x,y,z,\dots)$但与之并不相同的联合分布。如果我们可以从这个红色分布上抽样（即以$x$为控制变量做一次随机控制实验），那么这个问题也可以被有监督学习解决。然而，这不现实，我们仅有从蓝色的分布上抽样的数据。我们不得不去尝试从蓝色的分布上来估计条件概率$p(y|do(x))$。

因果模型

如果我们想要在蓝色分布与红色分布间建立联系，必须对数据产生机制的因果结构引入一些假设。只有在知道变量间因果关系的前提下，才能对干预后的分布做出预测。从联合分布来对因果关系建模是不够的，必须引入表达能力更强的工具。如下所示：

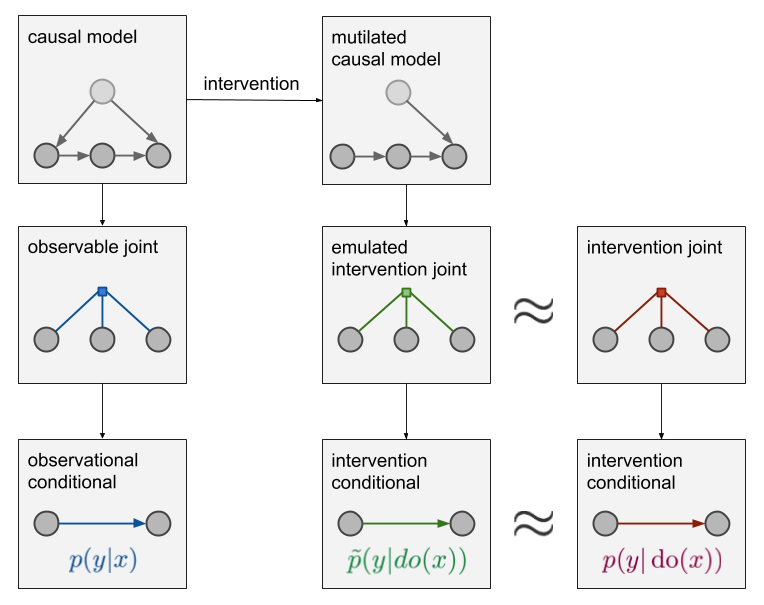
除联合分布外，我们现有还有一个因果模型（左上）。因果模型包含联合分布更多的细节：不仅知道压力和气压计显示值是由依赖关系的，而且知道这个依赖关系的确切结构。模型中的箭头意味着因果关系的方向，如果变量之间不存在箭头，则无因果关系。因果图和联合分布之间的映射是多对一关系：几个不同的因果结构可能具有相同的联合分布。因此，仅从观察数据获得确定唯一的因果结构是不可能的。

构建一个因果模型，我们必须考虑关于世界如何运行，什么造成了什么这样的假设。一旦我们有了一个因果图，我们可以通过改动因果图（删去所有指向$do$操作节点的边）对干预的结果进行仿真，如上图（中上）所示。绿色因子图就是这个改动过的因果图所对应的联合分布。相应的条件概率是$\tilde p(y|do(x))$，作为$p(y|do(x))$的近似。如果我们的因果结构是正确的，那么$\tilde p(y|do(x))=p(y|do(x))$。错误的因果结构假设会导致错误的近似结果。

为了得到绿色的部分来建立观察数据与干预结果之间的桥梁，我们不得不引入额外的假设，即先验知识。仅仅有数据是不够的。

do-算子

现在的问题是，我们在仅有蓝色分布数据的状况下，怎么有资格对绿色分布BB什么呢。比起之前将两者relating起来的因果模型，我们现在的状况已经好多了。长话短说，这就是“do-算子”的意义所在。在有蓝色分布的边缘、条件、期望等属性的情况，“do-算子”允许我们对绿色分布做个马杀鸡。”do-算子“通过引入4个额外的规则扩展了我们处理条件概率分布的工具箱。这些规则和因果图的属性相关，这篇博文无法将其全部阐明，但你可以读一下这篇入门论文。

理想情况下，“do-算子”的结果是一个公式$\tilde p(y|do(x))$，内部没有任何do操作，你可以在观察数据上单独估计它。这是$\tilde p(y|do(x))$可识别的情况。那么相反的，如果这是不可行的，无论我们怎么去尝试，也无法得到可识别的结果，这意味着我们无法从既有数据上去估计它。下面的图总结了因果推断机制 in its full glory。

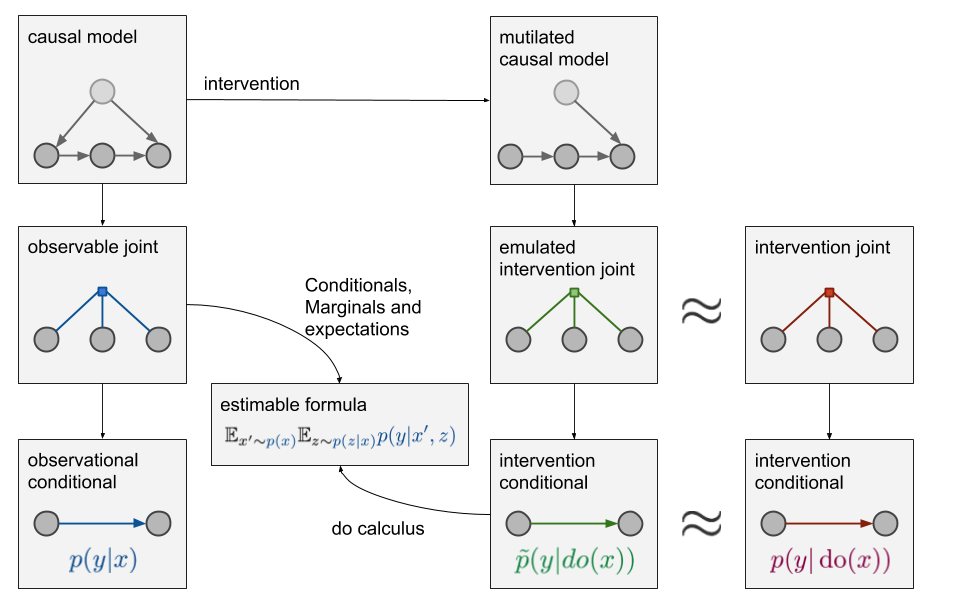
注意，如果你只关心$p(y|x)$ 那么变量$z$是完全是无关变量，你仍可以做有监督学习。但在因果推断中，如果我们不能观察到$z$，那么将不能够处理$p(y|do(x))$。

6 我怎么知道我的因果模型对不对？

你永远也无法从观测数据来充分验证一个因果模型的正确性和完整性。然而因果模型的一些aspects是可以通过实验验证的。具体来讲，因果模型蕴含着变量集之间的条件独立性和依赖关系。这些独立和依赖关系是可以被实验验证的，如果说你模型中的这些关系与数据相悖，说明你的因果模型是错的。带着这个观点你可以试着去做完整的因果发现：尝试从数据来推断因果模型，或者至少因果模型的一些aspects。

但底线是：a full causal model is a form of prior knowledge that you have to add to your analysis in order to get answers to causal questions without actually carrying out interventions. 单单依靠数据推理不能使你达到这一步。和贝叶斯推断不同，其先验知识是锦上添花并且可以提升数据效果的，而因果图对于因果推断是必须的。

7 总结

因果推断毫无疑问是很基础的东西。它可以让我回答”what-if-we-did-x”这样的问题，而这通常需要随即控制实验和精准的干预。 And I haven’t even touched on counterfactuals which are even more powerful.在一些情况下，你可以不关系因果推断。但存在一些应用场景，你必须使用因果推断才能解决问题。

我再次强调这篇博文不是关于你应该做因果推断还是深度学习。你可以，并且应该两者都做。 因果推断和“do-算子”可以让你理解问题并基于一些假设从数据中建立一个因果图模型。在实践中，你仍需要强大的工具（深度学习、SGD、变分等等）来帮助你完成工作。